Reciprocal - 4, 1/sin (x)

                        1                -1                    -1
 y = 1/sin (x) or  -------   or sin  (x)  or sin (x)
                       sin x

                                   -1

Oops !  This is wrong as sin  (x) is arcsin (x), which is the inverse (not reciprocal ) of sine function.

First reciprocal of sine function.

y = sin (x) is very familiar

sin (0) = 0

sin (π/4) = 1/√2

sin (π/2) = 1

sin (π3/4) =  1/√2

sin (π) = 0

sin (π5/4) =  - 1/√2

sin (π3/2) =  -1

sin (π7/4) = - √2

sin (2π) = 0

Therefore the reciprocals are

1/sin (0) = ?

1/sin (π/4) =  √2

1/sin (π/2) = 1

1/sin (π3/4) =  √2

1/sin (π) = ?

1/sin (π5/4) =  - √2

1/ sin (π3/2) =  -1

1/sin (π7/4) = - √2 

1/ sin (2π ) = ?

<?> is a big <?> as you will see soon.
 

                                             1

As the sin x is the denominator ------, when sin x approaches 0, the value becomes + ∞
                                                   sin x

 
or - ∞ . This is strange. 1/ sin (2π ) = ?

How about the graph ?  <sin x> is  -1 <  sin x < +1 or the min value -1.
                                                  =           =

                                                       1

As the sin x is the denominator ------, when sin x approaches 0, the value becomes + ∞

                                           sin x
 

or - ∞ . This is strange. <sin x> approaches 0 from 1/4 π it goes + ∞ while <sin x> approaches 0 from -1/4 π approaches it goes - ∞. You can see this in the following graph. How to interpret or explain this ?

See the graph. From Wiki.

          1
y =  -------
        sin x

 

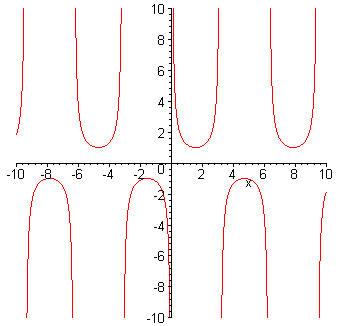
x- axis is radian. So at x = π/2(3.1415/2 = 1.5706) the value is 1 and x = π3/2 (3.1415x3/2 = 4.7123) the value is -1.

                                  1

As sin x is cyclical so is -------.

                                sin x

                                          -1

Now try to understand sin  (x) or arcsin (x) or a reverse function of sin (x).

        2

y = x

The reverse function of this is

        2

x = y

and then

y = +/- √x

x = 0 , y = 0

x = 1 , y = +/- 1

x = 2 , y = +/- √2

x = 4, y = +/- 2

x = 9, y = +/- 3

From Quora 

 

We already discussed this relation before in <Function of y = x>. This is a mirror image of y = x against y = x so <inverse> function. However 1/ sin x, though called <inverse>, is not a mirror image of y = x.

sin (π/4) = 1/√2

 

              -1

while sin (π/4) or arcsin (1/√2) = π/4  

In this sense y = arcsin (x) s called the <reverse>(relation) of y = sin (x).  

Confusing but the point is <π/4> of

sin (π/4) = 1/√2  is an angle (either in degree or in radian, radian is much more convenient) while <1/√2>is a ration  <1:√2>of the two line elements of a right triangle. On the other hand in<arcsin (1/√2) = π/4> an angle is a calculation result of the the ratio. Thai is all.   

Look at the graph of 

y = arcsin (x). 

I have found the following article. 

https://www.analyzemath.com/Inverse-Trigonometric-Functions/Arcsin.html 

 

y = arcsin(x) ⟺ x=sin(y)

This graph was made beautifully and shows clearly the function of the line y = x.


ACT