Saturday, August 8, 2020

Function of y = x


Function of y = x


 Or " demystifying  y = ln x ".


y = x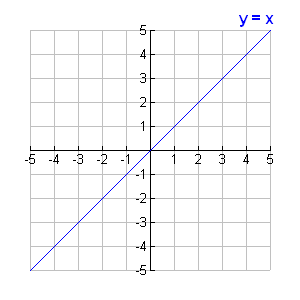

BIBLE CALCULUS – LIFE'S LESSONS

y = ex

and

y = ln x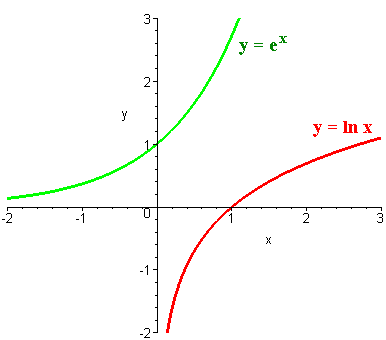


Logarithms


y = ln x is a mirror (reflected) image of  y = ex about y = x. Or you fold this chart (paper) along the line of y = x the red line is exactly on the green line. This is in 3D 180 degree rotation as y = x an axis. Or an ant starts waking from at any point of the red line to go toward the green line and takes the shorted distance to reach a point of the green line (by crossing the line of y = x at 90 degree angle or mathematically walk on the normal line ). This is ＜inverse＞relation. This may have a profound meaning. You can easily check this by using for instance

y = x +5 (or y = x + a, for more general)

y = x 2


It helps you to get an idea of ln x = y.

ln x = y

is, by definition

ey = x, which is the exchange of x and y in  ex= y( y = ex).


As a reminder

The mirror or reflected image of Point (x=2, y =5)  about y = x is Point (x=5, y = 2), which is easily found in the above chart of y = x. The function of y = x is great.


Additional insight to Function of y = x and e

I was stuck with following explanation found in ＜e (mathematical constant)＞Wiki.

”

In calculus

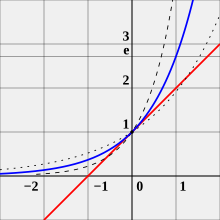
The graphs of the functions x ↦ ax are shown for a = 2 (dotted), a = e (blue), and a = 4 (dashed). They all pass through the point (0,1), but the red line (which has slope 1) is tangent to only ex there.

The value of the natural log function for argument e, i.e. ln(e), equals 1.


The principal motivation for introducing the number e, particularly in calculus, is to perform differential and integral calculus with exponential functions and logarithms.[16] A general exponential function y = ax has a derivative, given by a limit:

{\displaystyle {\begin{aligned}{\frac {d}{dx}}a^{x}&=\lim _{h\to 0}{\frac {a^{x+h}-a^{x}}{h}}=\lim _{h\to 0}{\frac {a^{x}a^{h}-a^{x}}{h}}\\&=a^{x}\cdot \left(\lim _{h\to 0}{\frac {a^{h}-1}{h}}\right).\end{aligned}}}

The parenthesized limit on the right is independent of the variable x: it depends only on the base a. When the base is set to e, this limit is equal to 1, and so e is symbolically defined by the equation:

{\frac {d}{dx}}e^{x}=e^{x}.


”

Wiki shows some more other ways to prove this

{\frac {d}{dx}}e^{x}=e^{x}.


This part of the wiki explanation has not changed much in last 10 years so that this is supposed be accepted by public. I read this part many times this time. The last part

＜When the base is set to e, this limit is equal to 1, and so e is symbolically defined by the equation＞

Of this part ＜When the base is set to e, this limit is equal to 1＞ is a kind of jumping to the conclusion unless you know that or why / how the this limit becomes 1. In case of general ＜a＞ when because h －＞0 ,


ah - 1               0 

----------  =    ----
    h                  0

which does not make sense. ＜symbolically＞ means in a way <damned important>. <defined by the equation＞. Is this just a definition, or truth ?

Another article (I read this article many times as well)

https://brilliant.org/wiki/derivatives-of-exponential-functions/

Derivatives of Exponential Functions

shows similar explanation but sticks to the general exponential and concludes

 d
---- ax  =  ax ln⁡ a
dx

{\frac {d}{dx}}e^{x}=e^{x}.





is symbolical.

 d
---- ax  =  ax ln⁡ a
dx


is symbolical too and more general since if you replace a with e you can get 

{\frac {d}{dx}}e^{x}=e^{x}.






Some one (https://rip94550.wordpress.com/2010/01/18/calculus-where-did-e-come-from/ and else) show an insight


"

{\displaystyle {\begin{aligned}{\frac {d}{dx}}a^{x}&=\lim _{h\to 0}{\frac {a^{x+h}-a^{x}}{h}}=\lim _{h\to 0}{\frac {a^{x}a^{h}-a^{x}}{h}}\\&=a^{x}\cdot \left(\lim _{h\to 0}{\frac {a^{h}-1}{h}}\right).\end{aligned}}}


This limit is <ln a>.


"

By definition ln e is simply 1.

But what does this mean ?  <ln a> can be seen as "the derivative factor of the general exponential " and is a logarithm with the base e (ln).



 d
---- ax  =  ax ln⁡ a
dx


Where did this come from ?

"
https://www.math24.net/derivatives-exponential-functions/

No(w) we consider the exponential function y=ax with arbitrary base a (a>0,a≠1) and find an expression for its derivative.


As a=eln a, 


then


ax=(eln a)x=ex ln a.


Using the chain rule, we have 


(ax)′=(ex ln a)′=ex ln a⋅(x ln a)′=ex ln a⋅ln a=ax⋅ln a.


Thus


(ax)′=ax ln a.


"


<chain rule> is a special case in this. But this special chain rule is shown in math text books.


But the point I want to make here is the first line

As a = eln a, 


This is almost a definition and also usually found in math text books. So it says " As a = e ln a ".
But remember the following I wrote above.

ey = x, which is the exchange of x and y in  ex= y( y = ex).

This is <reverse relation>.

ex is (natural) exponential function while ln a is (natural, base e ) is (natural) logarithm function.  ln a=e ln a, ln a is a power to e (e to the power ln a). This is in a way < inverse relation>. So intuitively e ln a becomes <a>.

Or if we use verbs
  
In ex ＜e＞is "exponetized" by ＜x＞ while in ln a ＜a＞ is "logaithmized" or ＜inversely exponentized＞by ＜e＞.

Likewise

in e ln a ＜e＞ is "exponetized" by ＜ln a＞by placed at this position. Since ＜a＞is "logarithmized" with base ＜e＞ by place after ln or ＜inversely exponentized＞by ＜e＞


e ln a becomes <a> after "logarthmized" "logarthmized""logarithimized or＜inversely exponentized＞ and then "exponetized" linking with ＜e＞ by＜e＞.
 

－－－－－

Wiki ＜exponential function＞says

"
Letting the number of time intervals per year grow without bound leads to the limit definition of the exponential function,

(ex =)  {\displaystyle \exp x=\lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}}

first given by Leonhard Euler.

"

but does not show how Euler found and gave it.

It is closely connected with the following definition / characteristic (one of the definitions / characteristics) :

(e =) \lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}.

Repeating

(ex =)  {\displaystyle \exp x=\lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}}


How to prove this. I found an answer (may be one of the answers) in the following article on the net.

＜e the EXPONENTIAL - the Magic Number of GROWTH＞ (good article)
https://www.austms.org.au/Modules/Exp/exp.pdf

As this is a pdf file it is difficult to copy / paste this part here. The method is a mathematically tricky one.

The exponent (power) part changes

           n                            n/x       x
(     )     --->  ( (     )      )

          x
( 1 + ---   )
          n

Please note the following tricky part.

           n                          n/x       x
(     )     --->  ( (     )      )

Then  n → ∞ .


               n/x 
 (     )     


This part becomes ＜e＞ by using

(e =) \lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}.


then we can get

(ex =)  {\displaystyle \exp x=\lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}}


The above is modified (so no copyright infringement but principally the same) and may be difficult to get it. Please go to the original

＜e the EXPONENTIAL - the Magic Number of GROWTH＞
https://www.austms.org.au/Modules/Exp/exp.pdf


ACT



Posted by at

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)