Thursday, July 23, 2020

Reciprocal - 3 (Taylor Series)



Reciprocal is somehow anti-intuitive. y = x is a very simple function, a simple straight line but its reciprocal : y = 1/x is not simple at all as shown below.




Apart from Electronics, I am recently re-studying "Taylor Series", which I studied before but highly likely did not understand it (as I do no remember what it is). In Wiki "Taylor Series" I found the following.

"
Definition
The Taylor series of a real or complex-valued function f (x) that is infinitely differentiable at a real or complex number a is the power series
{\displaystyle f(a)+{\frac {f'(a)}{1!}}(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+{\frac {f'''(a)}{3!}}(x-a)^{3}+\cdots ,}
where n! denotes the factorial of n. In the more compact sigma notation, this can be written as
{\displaystyle \sum _{n=0}^{\infty }{\frac {f^{(n)}(a)}{n!}}(x-a)^{n},}
where f(n)(a) denotes the nth derivative of f evaluated at the point a. (The derivative of order zero of f is defined to be f itself and (x − a)0 and 0! are both defined to be 1.)
When a = 0, the series is also called a Maclaurin series.[1]

"

Probably few people know the deep meaning (if it has).

Point 1)

{\displaystyle \sum _{n=0}^{\infty }{\frac {f^{(n)}(a)}{n!}}(x-a)^{n},}
where f(n)(a) denotes the nth derivative of f evaluated at the point a. ＜a＞is a certain x value but 
                                                                                                           n
related with f(a), of which derivatives becomes the coefficient of (x - a).  Also ＜/n!＞is necessary.

And (x − a)0 and 0! are both defined to be 1. - This is important but do not appear in the formula.

Probably few people know the deep meaning (if it has).


Point 2) 

(x - a) is the difference between x - a or distance between x and a. It may be close or may be far away. If x = a, (x - a) = 0. Taylor Series becomes 0 no matter what the front "Derivative Coefficient " and  ＜/n!＞are or Non sense! So should not be x = a.

(x - a) can be negative.

(-1) =(-1)

     2
(-1) = (+1)

     3
(-1) = (-1)

     4
(-1) = (+1)


Point 3)

It is clear that Taylor Series is closely related with the following "modern" definition of derivative (differentiation).

Wiki

This limit is defined to be the derivative of the function f at a:
f'(a)=\lim _{h\to 0}{\frac {f(a+h)-f(a)}{h}}.

Deep or hidden (if hidden) meaning it shows as both using <limit>.

Point 4)
 
Taylor Series is in general not used for the purpose of finding the function of f(x), but to show the already known f(x) in a Power Series form. So we may be able to call it Taylor (Series) Transform as well, like Fourier Series / Transform. f(x) in Taylor Series form may have some uses to deal with 
function f(x).
 
Let's go on with examples.
 
f (x) = x 
 
f (x)' = 1
f (x)'' = 0
 
When a = 0

                   1                    0               2
f (x) = 0 + ----- (x - 0) + ------- (x – 0) = x
                   1                    2
 
When a = 1

                   1                        0              2
f (x) = 1 + ----- (x – 1)   + ------- (x – 1) = x
                   1                        2


When a = 10

                      1                         0                2
f (x) = 10 + ----- (x – 10)  + ------- (x – 10)   =  x
                     1                          2
 

When a = - 2

                     1                     0          　　2
f (x) = -2 + ----- (x + 2) + ------　(x + 2)    =   x
                     1                    2

－－－－－
Examples from Wiki.

“
Examples

The Taylor series for any polynomial is the polynomial itself. 

The Maclaurin series for 1/(1 − x) is the geometric series. 
{\displaystyle 1+x+x^{2}+x^{3}+\cdots ,}
so the Taylor series for 1/x at a = 1 is
{\displaystyle 1-(x-1)+(x-1)^{2}-(x-1)^{3}+\cdots .}
“

This is our simple interest. Why ＜so＞ ? Simply change <x - 1> to x in 

 
　　　　　　　　　　2　　　　　3 　　　　　4
1 + (1 - x) + (1 - x) + (1 - x) + (1 - x) .....

                               2            2                       2         2
= 1 - (x - 1) + (x - 1) + (1 - x)((x - 1) + (x - 1)(x - 1)  .....

　　　　　　　　　　　　2　　　　 2 　　　　　　　　4
= 1 - (x - 1) + (x - 1) - (x - 1)(x - 1) + (x - 1) ....

　　　　　　　　　　　　2 　　　　3 　　　　4
= 1 - (x - 1) + (x - 1) - (x - 1) + (x - 1)



Copy -> paste does not work well here so I did some modification (the original meaning remains unchanged)


The Maclaurin series for 11 − x .

This part reads in Wiki

                                     1                  -1
The Maclaurin series for -------  or (1 - x)
                                          1- x 

    1                                             1
--------  seems quite similar to  ------  but the actual behavior seems quite differs.
 1 - x                                           x


When x = 0  the value is 1. 

                                         1
When x = 1 the value is -----, which does not exists or does not make sense.
                                         0

When x is in between ＜0 and 1＞,

x = 0 the value is 1.
x = 1/1000 or 0.001 the value is 1000/999 or 1.001001001 .... - almost 1.0
x = 1/100 or 0.01 the value is 100/99 or 1.010101.... - still almost 1.0
x = 1/10 or 0.1 the value is 10/9 or 1.11111....
x = 1/4 or 0.25 the value is 4/3 or 1.3333.....
x = 1/2 or 0.5 the value is 2
x = 3/4 or 0.75, the value is 4
x = 9/10 or 0.9 the value is 10
x = 99/100 or 0.99 the value is 100
x = 999/1000 or 0.990 the value is 1000

seems going to ∞ as x approaches to 1.

In case of more than 1 (dramatic change)

x = 1001/1000 or 1.001, the value is -1000
x = 101/100 or 1.01, the value is -100
x = 11/10 or 1.1, the value is -10
x = 3/2, the value is -2
x = 2, the value is -1
x = 3, the value is – ½
x = 10, the value is – 1/9
x = 100, the value is – 1/99
x = 1000, the values is – 1/999

seems closing to 0 as x goes on to +∞ while goes down to - ∞ as x approaches to 1.

While when x is negative,

x = -1/1000 the value is 1/1.001 or 0.9999..... or almost 1.0
x = -1/100 the value is 1/1.01 or 0.990000099..... or still almost 1.0
x = -1/10 the value is 1/1.1 or 0.90909090..... or almost 0.91
x = -1/4 the value is 4/5 or 0.8
x = -1/2 the value is 2/3 or 0.666666...
x = -3/4 the value is 4/7 or 0.5714285...
x = -9/10 the value is 10/19 or 0.526315
x = -1 the value is 1/2 or 0.5
x = -2 the value is 1/3
x = -10 the value is 1/9
x = -100 the value is 1/999
x = -1000 the value is 1/999 or 0.001001001.... almost 0

seems closing to 0 as x goes on to - ∞ .



                    1                                    1
Actually -------- is quite similar to ------ .
                1 – x                                   x

Look at the chart at the top.

x changes to -x, which means the x positive number becomes all negative while all negative numbers become positive. To make the two charts reflect along the y-axis. Then move these two charts horizontally by <1> to the right.  I cannot find the exact char of this. I found the following chart on the net. Please move the chart of

            1
y = - ---- horizontally by <1> to the right.
             x

1_6.png


https://www.yaklass.ru/p/algebra/8-klass/kvadratichnaia-funktciia-funktciia-y-k-x-11012/funktciia-y-k-x-ee-svoistva-i-grafik-9599/re-8a7d95fe-3694-42ed-973e-b5e769a7178d


Another chart I found on the net is similar but not exact either.


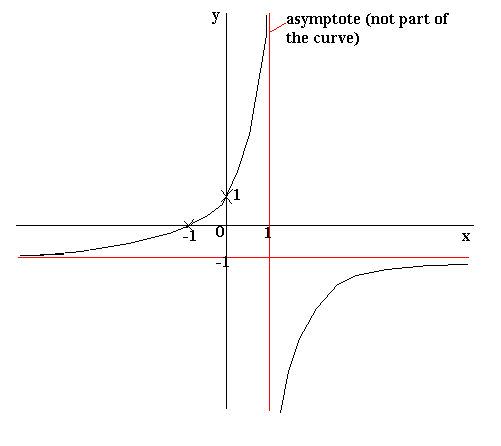
Curve Sketching - Mathematics A-Level Revision
 https://revisionmaths.com/advanced-level-maths-revision/pure-maths/geometry/curve-sketching

                                       1 + x
This is  the chart of y =  --------
                                      1 - x

when x = 2

       1 + 2
y = ----------  = - 3
       1 - 2

when x =3

       1 + 3
y = ----------  = - 2
       1 - 3

Differentiation is complicated but possible - Differentiation of quotient "quotient Rule".

Wiki

"
Let {\displaystyle f(x)=g(x)/h(x),} where both g and h are differentiable and {\displaystyle h(x)\neq 0.} The quotient rule states that the derivative of f(x) is
f'(x) = \frac{g'(x)h(x) - g(x)h'(x)}{[h(x)]^2}.
"


         1 + x
y =   --------
         1 - x

           1 (1-x) - (1+x)(-1)        1 - x +1 + x              2
y' =  ------------------------  =  ---------------  =  ----------------
            (1 - x) ^ 2                    (1 - x) ^ 2          (1 - x) ^ 2


At x being 0 the derivatives is 2.
At x being 2 the derivatives is also 2.

The slope of f(x) at x = 0 and 2.
You can see these on the chart. These correspond with chart.

But the other parts how to explain the relation between the equation and the chart ? We can guess the the charts move horizontally by ＜+1＞or to the right and vertically by ＜-1＞ or downward.

         1 + x
y =   --------
         1 - x

Modifying


                1 + x            1 + x +1 - x             2
y + 1  =   -------- +1 = -----------------   = ---------
                1 - x               1 - x                  1 - x


          2
y = --------   - 1
       1  -  x

                                                         2
This means vertically shifting  y = -------- downward by -1.
                                                      1 - x                     

We have already seen shifting horizontally to the right by 1.


Back to Wiki

                                                              -1
The Maclaurin series for 11 − x = (1- x)

Wiki does not give any explanation. The latter form is used for differentiation use - and we must use 'chin rule"

                     -1
f (x) =  (1- x)         

                        -2     
f (x) '  = -1(1 - x)  (-1) .       (-1)  comes from the differentiating (1 - x) ->  (1 - x) '  - as here required to use "chin rule"

                       -2
          =  (1 - x)

when x = 0 , it becomes 1

                        -3     
             -2(1 - x)     
f (x) ''  = ---------   (-1)
               2!

when x = 0 , it becomes 1

                         -4     
                - 6(1 - x)   
f (x) '''  =  --------   (-1) 
                 3!

when x = 0 , it becomes 1

                            -5     
                - 24(1 - x)
f (x) ''''  = -----------    (-1) 
                  4!

when x = 0 , it becomes 1

This process continues. Back to

{\displaystyle f(a)+{\frac {f'(a)}{1!}}(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+{\frac {f'''(a)}{3!}}(x-a)^{3}+\cdots ,}
and

The Maclaurin series for 11 − x is the geometric series

{\displaystyle 1+x+x^{2}+x^{3}+\cdots ,}


Our calculation above, a = 0. Please note

"
where f(n)(a) denotes the nth derivative of f evaluated at the point a.
"

which means

where f(n)(a) denotes the nth derivative of f (x) evaluated at the point x = a.  So in this case at x = a = 0

f (0) =1
f (0)' = 1
f (0)'' = 1
f (0)''' = 1
f (0)'''' = 1
.
.
.

So

The Maclaurin series for 11 − x is the geometric series

{\displaystyle 1+x+x^{2}+x^{3}+\cdots ,}

                                              1
Then when we put x = 0 in  ------
                                             1- x

   1
------  = 1
1 - 0

{\displaystyle 1+x+x^{2}+x^{3}+\cdots ,}  = 1   (x = 0)


Fine.


When we put x = 1/2

    1
---------  =  2
1 - (1/2)

1 + 1/2(=0.5)  + 1/4 (＝0.25) + 1/8 (＝0.125) + 1/16 (＝0.0625) + 1/32(＝0.03125) + 1/ 64 (＝0.0156) +　= 1.98435 + -->  2.0

Fine again.

 When we put x = 1

      1                1
   -------   =    -----
   1 - 1              0

While
1 + 1+ 1+ 1+1+ 1+ ........  = ∞ .  This may be correct as

when we put x －＞ 1


      1                          1
   -------------  =    ----------    = ∞ .  This may be correct.
   1 - x －＞1        －＞0

When we put x = -1/2

      1               2
   -------   =    -----  = 0.66666
   1 - (-1/2)     3

                          2         3            4          5
1+ (-1/2) + (-1/2)+ (-1/2)+ (-1/2) + (-1/2) + ......

= 1 - 0.5 + 0.25 - 0.125 + 0.0625 - 0.03125

= 0.65652

Fine again.


 When we put x = -1

      1                1
   -------   =    -----
   1 - (-1)          2


While  

                     2      3       4         5
1+ (-1) + (-1) + (-1)+ (-1) + (-1) + ......


                                                                                   0 + 1           1
= 1 -1 +1 -1 + 1 -1 + .....  = 0 or 1/2 or 1 ?  May be --------- =  ------
                                                                                     2               2

Again almost fine.
                                          9
How about x = - 0.9 or -  ------
                                         10

       1                          1             10
   ---------------  =     ------    =  ------- = 0.5263158
   1 - (- 9/10)           19/10         19


                         2           3          4           5             6           7            8            9          10
 1+ (-0.9) + (-0.9) + (-0.9)+ (-0.9) + (-0.9) + (-0.9) + (-0.9) + (-.0.9) + (-0.9) + (-0.9) ......

= 1 - 0.9 + 0.81 - 0.729 + 0.6561 - 0.59049 + 0.531441 - 0.4782969 + 0.43046721 - 0.387420489 +

0.2486784401

= 0.5914792611

If we continue we will approach 0.5263158, probably. So almost fine.


                                                                     99
One more step. How about x = - 0.99 or -  ------  ?
                                                                   100

       1                             1               100
   ------------------  =   --------    =  ------- = 0.50251256
   1 - (- 99/100)         199/100        199


                                2             3            4             5             6             7       
 1+ (-0.99) + (-0.99) + (-0.99)+ (-0.99) + (-0.99) + (-0.99) + (-0.99)

              8              9            10
 + (-.0.99) + (-0.99) + (-0.99) ......

= 1 - 0.99 + 0.9801 - 0.970299 + 0.96059601 - 0.9509900499 + 0.9414801494 - 0.9320653479 + 0.92274469442 - 0.91351723747 + 0.90438207499

This is roughly

= 1 - 0.99 + 0.98 - 0.97 +0.96 - 0.95 + 0.94 - 0.93 + 0.92 - 0.91 + 0.90

= 0.95 

and
                                                                                                                           11
= 1 - 0.99 + 0.98 - 0.97 +0.96 - 0.95 + 0.94 - 0.93 + 0.92 - 0.91 + 0.90 - (-0.99)  (= - 0.89533825424, roughly = - 0.895)

= 0.055

If we continue and continue and further continue it may converge to 0.50251256  probably as (095 +0.055) /2  = 5.025.

----------


It is not very intuitive to get

11 − x  = {\displaystyle 1+x+x^{2}+x^{3}+\cdots ,}

                        -2     
f (x) '  = -1(1 - x)     (-1) 

                        -2           1
          =  (1 - x)      =  ----------
                                            2
                                  ( 1 - x)

and

f(x) = {\displaystyle 1+x+x^{2}+x^{3}+\cdots ,}  

                                    2       3      4     
f ( x) ' = 0 + 1 + 2x + 3x + 4x + 5x  +  

are identical.

Furthermore the relation is not always correct either.

If x is more than 1 (excluding) , say x = 2

      1
   -------  =  -1
  1 - 2 

While

1 + 2 + 4 + 8 + 16 ...... is definitely not - 1.


Say x = 1.5 or 3/2

   1                1
 -------  =  -------   = - 2
1 - (3/2)     -1/2


1 -2 +4 - 8 + 16 - 32 + 64 + ......   ?  - highly unlikely becomes -2 

Say x = 1.01 or 101/100

      1                       1
 -------------  =   ---------  =  - 100
1 - (101/100)       -1/100
                                  
1 - 101/100 (=1.01) + 10201/10000(=1.0201) - 1,030,301/1,000,000(=1.030301) + 104,060,410/ 100,000,000(=1.04060) -

= 1.020399


Say x = 1.1 or 11/10

      1                       1
 -------------  =   ---------  =  -10
1 - (11/10)          - 1/10

while

1  + 1.1 + 1.21  + 1.331 + 1.4641+ .....


This relation can stand only a certain limited x value range, not an universal rule. Then which range ?
Probably ＜-1 - +1＞ by the above calculation of several representatives.


Next, back to Wiki

"

so the Taylor series for 1x at a = 1 is

{\displaystyle 1-(x-1)+(x-1)^{2}-(x-1)^{3}+\cdots .}
"

This should be

so the Taylor series for y or f (x) = 1x at a = 1 is

y or f (x)  = {\displaystyle 1-(x-1)+(x-1)^{2}-(x-1)^{3}+\cdots .}


if explained the process
     
        1        -1
y =  ---  =  x    = 1/1 = 1  (when x =1, which is a)
        x

            -2
y' = -1x      =  -1 (when x = 1)

The first derivative of y = 1/x  at x = 1 is -1 guessing from the chart.

           -3
y'' = 2x    = 2 (when x = 1)

             -4
y''' = -6x    = -6 (when x = 1)

.
.
.

                                          2                  3          
y (f (x)) =  1  - 1 (x - 1) + 2(x - 1)/2! - 6 (x - 1)/3! . . . .


= {\displaystyle 1-(x-1)+(x-1)^{2}-(x-1)^{3}+\cdots .}




Then when x =1

       1
y = ---- = 1
       1 


while

= {\displaystyle 1-(x-1)+(x-1)^{2}-(x-1)^{3}+\cdots .}

becomes
                            2        3
= 1 - (1-1) + (1-1) - (1-1) .....  = 1


Then when x =2

       1
y = ----
       2

= {\displaystyle 1-(x-1)+(x-1)^{2}-(x-1)^{3}+\cdots .}

becomes
                            2        3         4
= 1 - (2 - 1) + (2 - 1) - (2 - 1) +(2 - 1) ..... 

= 1 -1 +1 -1 + 1 .......   = 1 or 0 or 1/2


Then when x =3

       1
y = ----
       3

= {\displaystyle 1-(x-1)+(x-1)^{2}-(x-1)^{3}+\cdots .}

becomes
                            2         3          4
= 1 - (3 - 1) + (3 - 1) - ( 3- 1) + ( 3- 1) ..... 

= 1 -2 +4 - 8 + 16 - 32 + 64 .......   = ?




ACT
Posted by at No comments:
Subscribe to: Posts (Atom)