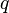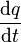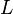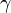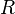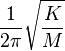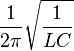Capacitance, Inductance and Time

The title is "Capacitance, Inductance and Time " but "Time" here is used as Frequency. The unit of Frequency is Hz as well as 1/s (1/t in symbol).


The relations between Capacitance and Frequency, Inductance and Frequency are commonly stated as below usually with no explanation.

 

or no <minus sign>

 and




Two (2) very simple calculations lead to the above two equations.


1) Capacitance and Frequency

where X is Capative Reactance (Xc)

This relationship can be derived from the following basic Capacitor equation related with i and v.

Rearranged

i (t) x dt 
---------- =  C
dv(t)

as I/V (or i/v) = 1/R

t/R = C

R = t/C

as Frequency (f) is 1/t or t = 1/f

R = 1/Cf

where R can be regarded as Xc and f is used as Frequency in general.  ω = 2πf

We need some conceptional jump to get into another world of frequency domain.


2) Inductance and Frequency

Likewise,

where XL is Indcutive Reactance.

This relationship can be derived from the following basic Inductor equation related with i and v.



Rearranged

v (t) x dt 
---------- =  L
di(t)

as V/I (or v/i) = R

tR =L

R = L/t

as Frequency (f) is 1/t or t = 1/f

R = Lf

where R can be regarded as XL.


Here again we need some conceptional jump to get into another world of frequency domain.


ACT

Capacitance and Inductance as Inertia

Capacitance (C) and Inductance (L) as Inertia - against the change

Mass as related to 'inertia' of a body can be defined by the formula:

F = ma 

This can be rearranged as F/m = a. So m can be considered as against acceleration, which means against the change of velocity.

Capacitor analogy

This can be rearranged as i(t)/C = dv(t)/dt. So like m against F, C can be considered as against dv(t)/dt. Against dv(t)/dt means against the change of voltage.

CV = Q  (cv = q)
Q/C = V (q/v = v)

Quote from Physical Properties Chart - Tom Potter's World

"
Contrary to intuition, charge is stored by stressing the dielectric rather than in a pool of charges. When stressed by the application of a voltage, a good dielectric material remains in the stressed state longer than an ordinary insulator, and there is little charge movement (Leakage) across it. A dielectric can be compared to a spring. A dielectric stores an electrical stress (Voltage) whereas a spring stores mechanical stress (Force).
"

F = -kx

F: Restoring Force corresponding to the applied Force
k: spring constant
x: displacement

F can be considered as an applying Force, which is equal to -kx where <k> is Newton/meter. Then <kx> is Force (in Newton) and has the same magnitude as but is in the opposite direction of F.

When F is analogous to V , 1/C is analogous to <k> and <x> to Q (charge). Q/C = V

Inductor analogy

This can be rearranged as v(t)/L = di(t)/dt. So So like m against F, L can be considered as against di(t)/dt. Against di(t)/dt means against the change of current.

As the current is the time rate change of charge q or i(t) = dq(t)/dt. This is more like F/m = a as a (acceleration) is the time rate change of v (velocity) and v (velocity) is the time rate change of distance (more precisely displacement) d or  v (velocity) = dd(t)/dt. Charge q is not a distance (displacement) but a certain quantity, can be analogous to F/m = a and shows its dynamical nature (not static) - flow or motion of charge q, not static position or quantity like as in a capacitor.

Further analogy

From Wiki <Harmonic Oscillation> 09-Nov-2015

"

Translational Mechanical	Series RLC Circuit
Position	Charge
Velocity	Current
Mass	Inductance
Spring constant	Elastance
Damping	Resistance
Drive force	Voltage
Undamped resonant frequency
Differential equation:

"

The above are common analogies. I would say "beautiful analogy".

<x> is not just <position> but <displacement>. And <x> and <q> are not easy to be connected analogically.

Inductance is analogous to Mass (Inertial Mass). Very clear.

More precisely <->(minus sign) is required before <L>.

<Elastance> is a simply the reciprocal of Capacitance. Analogically <Elastance>, as the name suggests, is the unit showing <Elasticity> and roughly the reciprocal of <Stiffness>.

Let's review <displacement> to connect <charge> analogously.

The Penguin Dictionary of Physics says:

Displacement is

1. A vector representing in magnitude and direction the difference in position of two points. It is the basic vector used in physics. Velocity is defined as rate of change displacement, acceleration is rate change of velocity. Thus mechanical quantities such as MOMENTUM and force, and electrical quantities such as ELECTRICAL FIELD depend upon the concept of displacement.

2. The quantity of fluid displace by submerged or partly submerged body.

3. See ELECTRIC DISPLACEMENT

-----

ELECTRIC DISPLACEMENT is rather complicated to understand and to be convinced. The unit is coulomb / meter squared, which may be considered as a density on (though) the surface (surface density) of charge. Though <charge> is involved but difficult to relate with the mechanical displacement (the difference in position of two point) analogously.

The Penguin Dictionary of Physics says:

Electrical displacement is

---- the electric flux per unit area ( electric flux density) in the medium.




ACT

Mystery of "Power = V x I" - (2) or 'Q' Magic

This article is a continuation of Mystery of "Power = V x I" (posted on 6/24/11). Since the last post was very short I will repeat it below:

"
V (Joule/Coulomb) x I (Coulomb/second) = Power (Joule/sec = Energy/sec). So after multiplication of V by I, Coulomb (unit of electric charge) disappears like a magic and only Energy and time remain. This explains well that Current is not consumed in a load such as a resistor and a light bulb - Kirchhoff's Current law but Energy is consumed, changed to some other form of Energy - conservation of Energy.

"

I want to call it 'Q' magic, not a Quantum Magic but Charge Magic. We now think it further in terms of Energy.

I wrote in the first article in Asnet Tutorial as follows:

"

Energy/Q = V ---> Energy = QV

Energy/ Φ = I ---> Energy = ΦI

Energy x Energy =QV x ΦI = VI x QΦ

= VI x <I x time> x <V x time>

Therefore

Energy² = (VI x time)²

Energy = +/- VI x time

This helps us to what Power (VI) means in terms of Electric and Magnetic Fields.

"

In the above explanation Q plays a vital role but Q disappears in the final equation - Energy = +/- VI x time (this should by Energy = VI x time as no negative Energy).

Energy/Q = V ----> Energy = QV

Energy/ Φ = I ----> Energy = ΦI

These two equations are actually the same thing although QV seems (electro)static and ΦI seems (magneto) dynamic because

Energy = QV = (I x time) x V

Energy = ΦI = (V x time) x I

We can think of two different conditions - time stops and time is passing. When time stops it becomes static while time is passing it becomes dynamic in either electrically or magnetically. When static the energy becomes potential while when dynamic (the values changes with time) the energy becomes non-static or status of the energy changes.

Energy = QV = (I x time) x V

Although I is a scalar value (Q/t) Qs move (flow) V may unchanged or varies with time when dynamic.

Energy = ΦI = (V x time) x I

V does not move but changes with time and I may unchanged or changes with time and Qs move (flow) when dynamic.





By using the above two equations we can get also

Power = VI = Energy x Energy/QΦ

Here again Q = I x time , Φ = V x time

Very simple. These equations are very simple but they have 'meanings' and maybe 'profound meanings"

What is Gradient ? - 3

What is Gradient ? - Continuation -2
 

The recent wiki (29-Sept-20202) on Gradient is much deeper and more general (broader meanings from more different aspects)  but still does not explain "why the steepest (fastest, quickest)?".

"

Cartesian coordinates

In the three-dimensional Cartesian coordinate system with a Euclidean metric, the gradient, if it exists, is given by:

${\displaystyle \nabla f={\frac {\partial f}{\partial x}}\mathbf {i} +{\frac {\partial f}{\partial y}}\mathbf {j} +{\frac {\partial f}{\partial z}}\mathbf {k} ,}$

where i, j, k are the standard unit vectors in the directions of the x, y and z coordinates, respectively.

"

The explanation on the above has become just a part of <much deeper and more abstract > explanation.

For instance,

"
The gradient is dual to the derivative : the value of the gradient at a point is a tangent vector – a vector at each point; while the value of the derivative at a point is a cotangent vector – a linear function on vectors.^[c] They are related in that the dot product of the gradient of f at a point p with another tangent vector v equals the directional derivative of f at p of the function along v; that is, .

The gradient vector can be interpreted as the "direction and rate of fastest increase". If the gradient of a function is non-zero at a point p, the direction of the gradient is the direction in which the function increases most quickly from p, and the magnitude of the gradient is the rate of increase in that direction.
"

We may be able to explain "why the steepest (fastest, quickest)?" by some other ways with deeper meanings.

sptt

What is Gradient ? - 2, Primitive understanding

What is Gradient ? - Continuation

In the previous post on Gradient <What is Gradient ? Basic understanding>, I introduced as

Wiki (26-Jan-2012) introduces gradient as

"
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is that rate of increase.

"

It is more like a definition, not an explanation to those who do not know gradient well. But this is not a definition. Many simple articles on gradient do not explain why so. Some articles explain why by using "directional derivative" but the explanations are roundabout and we must understand first what "directional derivative" is before understanding gradient.

Notes: 

1) the greatest rate of increase of the scalar field

 Please note that this is not  <the greatest increase of the scalar field>

As the definition-like statement above talks of scalar field and vector field then we must think every possible point (all possible points) and every tiny time (down to the limit) when we talk and think of a field. But here we can forget time and focus on only space and scalar values at all possible points which are regarded as a scalar field as a whole and change it to a vector field to see things differently.

The key word or concept is <points>, which exist in /on 1D and 2D and in 3D. Each point has zero dimension (0D) or is in zero dimension (0D) or a point itself is zero dimension (0D).

First, consider the distance between the two points.

    Point A    ---->   .                .  <--- point B

The distance is obvious.

Second, consider the distance between a point and straight line.


    Point A    ---->   .  

    _______________________    Line B

There are many distances but the shortest distance is 

Point A    ---->   .  
                           l
                           l
                           l____________    Line B

The length of the perpendicular straight line from the point Point A to the line B.

This is also obvious.

Third, we consider a curve

Point A   .  -----> c <--- curve C

Point A    ---->   .  
                           l
                           l
                           l
                            .     <---- Point B  and tangent line
                 -                 -                             
         -                                 -               <--- curve C   (please try to see these points as a curve.
   -                                             -                  

 
We can consider the shortest distance from Point A to curve C is the length of the perpendicular straight line from the point Point A to the curve C. We find point B on the tangent line

Forth, we can do the same thing - the shortest distance from a point to a surface, wither flat or curved space. I do not show it here but if we cut a surface properly we see the above figure.

The key word or concept is <the perpendicular straight line>. This (the shortest distance from a point to another point is  <the perpendicular straight line>) is considered to be obvious at this primitive stage of understanding gradient. Perpendicular straight lines are used in gradient calculation but largely hidden because they are obvious.

We may be able to consider this <the perpendicular straight line> as < the greatest (fastest) rate of increase of the scalar field> not because this is obvious but because

1) the the length of shortest straight line is regarded as the fastest space rate change of  the scalar values the two different points.

2) 1) is analogous to the fact the the shortest time to travel a certain distance or move  from one point to the other point is regarded as the fastest time rate change of the movement.


-------------

The introduction of wiki (11-Sept-2015) on "directional derivative" says

"
In mathematics, the directional derivative of a multivariate differentiable function along a given vector v at a given point x intuitively represents the instantaneous rate of change of the function, moving through x with a velocity specified by v. It therefore generalizes the notion of a partial derivative, in which the rate of change is taken along one of the coordinate curves, all other coordinates being constant.

"

The last part <a partial derivative, in which the rate of change is taken along one of the coordinate curves, all other coordinates being constant.> may give us a hint but again roundabout we must understand first what "coordinate curves" are.


Common explanation and equation of gradient

Also from wiki on gradient (11-Sept-2015)

"
In the three-dimensional Cartesian coordinate system, this is given by

where i, j, k are the standard unit vectors.
"

When we use this we can re-write the above

"
<a partial derivative, in which the rate of change is taken along one of the Cartesian coordinate system, all other coordinates being constant.>

"

Tangent and tangent line

We must recall a tangent line (not a plane) of a 2D function of x, y,  f (x, y). The tangent line shows the slope (the result of differentiation) of the curve at the point P where the tangent line and the curve meets at one point (place). The place must be only one point otherwise the line does not touch the curve but departs from or crosses the curve. The slope (tangent) is usually measured as a ratio of 'b' to 'a' of a triangle. Tangent is a ratio,  taking 0 (zero) to infinite (∞, -∞), not a degree of angle. 


                          /l
                        /  l
                      /    l
                c  /      l   b
                  /        l
                /          l
              /            l
            /_______l 
                  a (1)     


                                 b
tangent (angle) =    ----
                                a

or more mathematically by using the unit length (one) of 'x' to 'y' length with  of a triangle the direction from the x-axis (horizontal) to the y-axis which is vertical to the x-axis or in another word differs by 90 deg or 1/2π from x-axis counter-clock wise, and sin (1/2π) is 1 and cos (1/2π) is 0 (zero). In this case (Cartesian coordinate system) we can show a direction with x-axis direction, y-axis direction and z-axis direction in 3D. The important thing is x-axis, y-axis and z-axis are mutually perpendicular and these axes are straight lines.

Multivariable equation

The other thing which we must have some concept about for understanding gradient is the multivariable equation.

Multivariable equation is usually expressed as

f (x, y)
f (x, y, z) 
f (x, y, z, ...) 

For instance,

f (x, y) = x + y or f  is a function of <x plus y>.  x and y are variable and can take any value.

x = 0, y = 0,  f (x, y) = 0
x = 1, y = 0,  f (x, y) = 1
x = 0, y = 1,  f (x, y) = 1
x = 1, y = 1,  f (x, y) = 2

Let's do some more.

y = 0

x = - 3, y= 0,  f (x, y) = -3
x = -2, y= 0,  f (x, y) = -2
x = -1, y= 0,  f (x, y) = -1
x = 0, y= 0,  f (x, y) = 0
x = 1, y= 0,  f (x, y) = 1
x = 2, y= 0,  f (x, y) = 2
x = 3, y= 0,  f (x, y) = 3

x = - 0.1, y= 0,  f (x, y) =  - 0.1
x = - 1/3, y= 0,  f (x, y) = - 1/3 (-0.33333....)
x = -0.5, y= 0,  f (x, y) = - 0.5
x = 0, y= 0,  f (x, y) = 0
x = 0.1, y= 0,  f (x, y) =  0.1
x = 1/3, y= 0,  f (x, y) =  1/3 (0.33333....)
x = 0.5, y= 0,  f (x, y) =  0.5

x = 0

x = 0, y= -3,  f (x, y) = -3
x = 0, y= -2,  f (x, y) = -2
x = 0, y= -1,  f (x, y) = -1
x = 0, y= 0,  f (x, y) = 0
x = 0, y= 1,  f (x, y) = 1
x = 0, y= 2,  f (x, y) = 2
x = 0, y= 3,  f (x, y) = 3

y = 1

x = -4, y = 1,  f (x, y) = -3
x = -3, y = 1,  f (x, y) = -2
x = -2, y = 1,  f (x, y) = -1
x = -1, y = 1,  f (x, y) = 0
x = 0, y = 1,  f (x, y) = 1
x = 1, y = 1,  f (x, y) = 2
x = 2, y = 1,  f (x, y) = 3


x = 1

x = 1, y= -4,  f (x, y) = -3
x = 1, y= -3,  f (x, y) = -2
x = 1, y= -2,  f (x, y) = -1
x = 1, y= -1,  f (x, y) = 0
x = 1, y= 0,  f (x, y) =  1
x = 1, y= 1,  f (x, y) = 2
x = 1, y= 2,  f (x, y) = 3

Very simple and primitive, monotonous and a lot of freedom. No special meaning, isn't it ?  

y = x

This is a very primitive function as well.  We can change this to a form of f (x, y).
 
f (x, y) = y - x = 0

But this is misleading as f (x, y) can be regarded as  f (x, y) = y - x or f (x, y) = y - x = 0 as above. The latter means  f (x, y) is <y - x = 0>. So there are two possibilities.

1) f (x, y) = y - x and 2) f (x, y): y - x = 0

1)  f (x, y) = y - x

This is quite general as x and y can take any number in the range of <-∞> through <0> to <+ ∞> and calculate it and get a result (number). This is also rather abstract or like playing with numbers.

y = 0

x = - 3, y= 0,  f (x, y) = 3
x = -2, y= 0,  f (x, y) = 2
x = -1, y= 0,  f (x, y) = 1
x = 0, y= 0,  f (x, y) = 0
x = 1, y= 0,  f (x, y) = - 1
x = 2, y= 0,  f (x, y) = - 2
x = 3, y= 0,  f (x, y) = - 3

Of course we can take +/-0.1, +/- 1/3, +/-0.5, etc up to +/- 1.

x = - 0.1, y= 0,  f (x, y) =  0.1
x = - 1/3, y= 0,  f (x, y) = 1/3 (0.33333....)
x = -0.5, y= 0,  f (x, y) = 0.5
x = 0, y= 0,  f (x, y) = 0
x = 0.1, y= 0,  f (x, y) = - 0.1
x = 1/3, y= 0,  f (x, y) = - 1/3 (0.33333....)
x = 0.5, y= 0,  f (x, y) = - 0.5

some more

x = 0

x = 0, y= -3,  f (x, y) = -3
x = 0, y= -2,  f (x, y) = -2
x = 0, y= -1,  f (x, y) = -1
x = 0, y= 0,  f (x, y) = 0
x = 0, y= 1,  f (x, y) = 1
x = 0, y= 2,  f (x, y) = 2
x = 0, y= 3,  f (x, y) = 3

y = 1

x = -3, y = 1,  f (x, y) = 4
x = -2, y = 1,  f (x, y) = 3
x = -1, y = 1,  f (x, y) = 2
x = 0, y = 1,  f (x, y) = 1
x = 1, y = 1,  f (x, y) = 0
x = 2, y = 1,  f (x, y) = -1
x = 3, y = 1,  f (x, y) = -2
x = 4, y = 1,  f (x, y) = -3
x = 5, y = 1,  f (x, y) = -4

x = 1

x = 1, y= -2,  f (x, y) = -3
x = 1, y= -1,  f (x, y) = -2
x = 1, y= 0,  f (x, y) = -1
x = 1, y= 1,  f (x, y) = 0
x = 1, y= 2,  f (x, y) = 1
x = 1, y= 3,  f (x, y) = 2
x = 1, y= 4,  f (x, y) = 3


Can we find anything particular in this fairly general equation?  Maybe some symmetries.
As up to here very numerical, mechanical, monotonous or abstract we visualize them by using a graphs, relatively simple in this case. How to visualize these ?

We can plot f (x, y) on a common x-y plane (Cartesian coordinate) as showing the location.

f (x, y) = x - y

y = 0

x = - 3, y= 0,  f (x, y) = 3
x = -2, y= 0,  f (x, y) = 2
x = -1, y= 0,  f (x, y) = 1
x = 0, y= 0,  f (x, y) = 0
x = 1, y= 0,  f (x, y) = - 1
x = 2, y= 0,  f (x, y) = - 2
x = 3, y= 0,  f (x, y) = - 3

<x-y locations>

                         y
                             l 
                             l
                             l
                             l
  -3     -2     -1       l 0      1      2       3

--*-----*-----*-----*-----*-----*-----*--------
                             l                                x
                             l   
                             l     
                             l
                      

But where to put the result of the equation: 3, 2, 1, 0, -1, -2, -3.

If we put these results on x-axis, it becomes very confusing and wrong as these number are not the value of x but the value of the calculation results of f (x, y) = x - y and when y = 0. Putting these results on y-axis is also wrong by the same reason.

We can draw a line showing the plot on another independent line from the line of  f (x, y) = x - y.

Result

   -3      -2     -1       0      1       2       3
---*-----*-----*-----*-----*-----*-----*---- 

One more

f (x, y) = x - y

x =1

x = 1, y= -2,  f (x, y) = -3
x = 1, y= -1,  f (x, y) = -2
x = 1, y= 0,  f (x, y) = -1
x = 1, y= 1,  f (x, y) = 0
x = 1, y= 2,  f (x, y) = 1
x = 1, y= 3,  f (x, y) = 2
x = 1, y= 4,  f (x, y) = 3

<x-y locations>

                         y
                   l          l    
                   l         *  4
                   l          l       
                   l         *  3
                   l          l    
                   l         *  2
                   l          l     
                   l         *  1
                   l          l   

--------------------- *-------------
                0 l    1    l                    x
                   l         *  -1
                   l          l  
                   l         *  -2
                   l          l         
                   

Result shown on another independent line


   -2      -1      0       1       2       3      4
---*-----*-----*-----*-----*-----*-----*---- 


Possible but difficult to co-relate the position (location) of (x, y) and the results of f (x, y) = x - y.

One of the many ways to visualize the co-relation between the location and the resulting value is to show the results as z-value of z-direction, which is perpendicular to the x-y plane as a rule.

The first one above f (x, y) = x - y, y = 0

The result can be shown as below.

^  z
l

  *(3)
       
           * (2)
              
                    * (1)
  -3     -2      -1      0       1       2       3

--*-----*-----*-----*-----*-----*-----*-------- 
                               (0)                                 x
                                      * (-1)
                   
                                             * (-2)
                                                  
 l                                                      * (-3)
V   z 


As y = 0 (constant) we can draw a graph in 2D (x-z plane). You can connect (3) - (2) - (1) - (0) - (-1) - (-2) - (-3) by a line.

Now we think of the slope (tangent) of this line on the x-z plane. It is simple and that is <-1>.

The second one

<f (x, y) = x - y line>, x = 1

The result can be shown as below.

^  z
l

  *(3)
       
           * (2)
              
                    * (1)
   4       3      2       l       0      -1      -2

--*-----*-----*-----*-----*-----*-----*-------- 
                               (0)                                 y
                                      * (-1)
                   
                                             * (-2)
                                                  
 l                                                      * (-3) 
V   z 

As x = 1 (constant) we can draw a graph in 2D (the y-z plane shifted by + 1x). You can connect (3) - (2) - (1) - (0) - (-1) - (-2) - (-3) by a line. Again we think of the slope (tangent) of this line on the y-z plane and again we get <-1>.

Then we think of <gradient> concept. The z values can be considered as some scalar values (height, temperature).

Height is somewhat misleading as z value can be taken as height of the 3D. But this is true. So let's consider the z value shows the height at a certain specified location on the x-y location, specified by the values (numbers) of x and y of the function f (x, y). The slope simply means slope. Meanwhile y = 0 so on either x-y plane or y-z plane the slope of y to x or z is zero intuitively.

Now we use the gradient formula shown at the beginning.

f (x, y) :  x - y = z  -->  x - y - z = 0

Grad f (x, y, z) = Grad  (x - y - z) 

When y = 0  (constant)

(dx/dx) i + (d(-y)/dy) j  - d(-z)/dz)) k =  1i - 0j - 1k

1i - 1k　 ---> This shows

1) a vector showing a direction (i, j, k are unit vectors and mutually perpendicular as a rule)
2) the slope is <-1> on x-z plane (also as shown in the above graph)
3) the magnitude is √2 .


The other example shown above.

f (x, y) = x - y = z ---> f (x, y) = x - y - z = 0

Grad f (x, y, z) = Grad  (x - y - z)

When x =1 (constant)

0 i + (d(-y)/dy)) j  - d(-z)/dz)) k =  0i - 1j - 1k

1j - 1k　   ---> This shows

1) a vector showing a direction
2) the slope is <-1> on y-z plane (also as shown in the graph below)
3) the magnitude is √2 .

The gradient formula seems to work though we are in a very simple or quasi 3-D space as y = 0 (constant) and x = 1 (constant). We can get more lines by changing the value of x other than <0>, the value of y other than  <1> though still these values of x and y are constant.
We can play with numbers and graphs and may get some meanings if we continue. But we change to 

2) f (x, y): y - x = 0

This is lot more restricted than f (x, y) = y - x. In this case the values (numbers) of x and y must satisfy this equation so we cannot take any value (number) we like. In other words <=0> has a significant role.

When y = -3, x must be -3
When y = -3, x must be -2
When y = -1, x must be -1
When y = 0, x must be 0
When y = 1, x must be 1
When y = 2, x must be 2
When y = 3, x must be 3

i.e. x must be equal to y or y must be equal to x as y and x are treated as independent and dependent mutually in case f (x, y): y - x = 0. This is a big restriction or constrain or rule which we cannot break or change. 

And we can think of  

f (x, y): y - x = z = 0

As z = 0,  f (x, y): y - x = 0 is on the x - y plane, i.e. 2D.

 

            y   l         /  <--   y - x = 0 or y = x at z = 0
                 l       /
                 l     /
                 l   /
                 l /
________ l ________
               / l                 x
             /   l       
           /     l         
         /       l            
       /         l            



We apply <gradient>

Grad (y - x - z)

z = 0

(dy/dy) j + (d(-x)/dx) i + 0k  = j - i

The slope of the gradient of y - x = 0 is <-1>

A very interesting thing is that the original equation y - x = 0 or y = x. The slope is <+1>. Simple thing but the slope of the gradient of y - x = 0  is <-1> which is perpendicular to the slope <+1>.


One more sample.

y= x²

We change this to a form of f (x, y),

f (x, y) = y - x² = 0

But this is misleading as f (x, y) can be made as  f (x, y) = y - x² or f (x, y) = y - x² = 0 as above. The latter means - f (x, y) is y - x² = 0. So again there are two possibilities.

1) f (x, y) = y - x² and 
2) f (x, y) : y - x² = 0

1) f (x, y) = y - x²

This is quite general as x and y can take any numbers in the range of <-∞> through <0> to <+ ∞> and calculate and get a result (number). This is also rather abstract or playing with number.

x = - 3, y= 0,  f (x, y) = -9
x = -2, y= 0,  f (x, y) = -4
x = -1, y= 0,  f (x, y) = -1
x = 0, y= 0,  f (x, y) = 0
x = 1, y= 0,  f (x, y) = -1
x = 2, y= 0,  f (x, y) = -4
x = 3, y= 0,  f (x, y) = -9

Of course we can take +/-0.1, +/- 1/3, +/-0.5, etc up to +/- 1.

x = - 0.1, y= 0,  f (x, y) = -0.01
x = - 1/3, y= 0,  f (x, y) = - 1/9 (0.011111....)
x = -0.5, y= 0,  f (x, y) = - 0.25
x = 0, y= 0,  f (x, y) = 0
x = 0.1, y= 0,  f (x, y) = - 0.01
x = 1/3, y= 0,  f (x, y) = - 1/9
x = 0.5, y= 0,  f (x, y) = - 0.25

some more

x = 0, y= -3,  f (x, y) = -3
x = 0, y= -2,  f (x, y) = -2
x = 0, y= -1,  f (x, y) = -1
x = 0, y= 0,  f (x, y) = 0
x = 0, y= 1,  f (x, y) = 1
x = 0, y= 2,  f (x, y) = 2
x = 0, y= 3,  f (x, y) = 3

x = -3, y = 1,  f (x, y) = -8
x = -2, y = 1,  f (x, y) = -3
x = -1, y = 1,  f (x, y) = 0
x = 0, y = 1,  f (x, y) = 1
x = 1, y = 1,  f (x, y) = 0
x = 2, y = 1,  f (x, y) = -3 
x = 3, y = 1,  f (x, y) = -8 

x = 1, y= -3,  f (x, y) = -4
x = 1, y= -2,  f (x, y) = -3
x = 1, y= -1,  f (x, y) = -2
x = 1, y= 0,  f (x, y) = -1
x = 1, y= 1,  f (x, y) = 0
x = 1, y= 2,  f (x, y) = 1
x = 1, y= 3,  f (x, y) = 2
x = 1, y= 4,  f (x, y) = 3
x = 1, y= 5,  f (x, y) = 4 

We can play with numbers and may get some meanings if we continue. But we change to 

 2) f (x, y) : y - x² = 0
 
This is a lot more restricted than f (x, y) = y - x². In this case the values (numbers) of x and y must satisfy this equation so we cannot take any value (number) we like. In other words <= 0> has a significant role.

When y = 0, x must be 0
When y = 1, x must be +/- 1
When y = 2, x must be +/- √2
When y= 3, x must be +/- √3
When y= 4, x must be +/- 2

To differentiate y= x² with respect to 'x' we get

 y = 2x

which shows the slope or tangent (ratio of y to x or y/x) of y= x² at any point of / on y= x². 

When x = 0, y = 0
When x = 1, y = 2
When x = -1, y = -2 
When x = 2, y = 4
When x = -1, y = -4
When x = 3, y = 9
When x = -3, y = -9

which means

At (0, 0) of / on y= x²  the slope is 0. we cannot calculate y/x but can easily guess.
At (1, 1) the slope is 2.
At (-1, 1) the slope is -2
At (2, 4) the slope is 4
At (-2, 4) the slope is -4
At (3, 9) the slope is 9
At (-3, 9) the slope is -9

Now we partially differentiate f (x, y),    

f (x, y) = y- x²

First with respect "only" to 'x' 

f 'x(x, y) = y -2x

At the point (0, 0),  f ' x(0, 0) = 0 -2 x 0 = 0

At the point (1, 1),  f 'x(1, 1) = 1 -2 x 1 = -1

At the point (-1, 1),  f 'x(-1, 1) = 1 -2 x (-1) = 3 

At the point (2, 4),  f 'x(2, 4) = 4 - 2 x 2 = 0

At the point (-2, 4),  f 'x(-2, 4) = 4 -2 x (-2) = 8

At the point (3, 9),  f 'x(3, 9) = 9 - 2 x 3 = 3

At the point (-2, 4),  f 'x(-2, 4) = 9 - 2 x (-2) =13

Now with respect "only" to 'y'

f 'y(x, y) = 1 - x²

At the point (0, 0),  f ' x(0, 0) = 1 - 0 = 1

At the point (1, 1),  f 'x(1, 1) = 1 - 1 x 1 = 0

At the point (-1, 1),  f 'x(-1, 1) = 1 - (-1) x (-1) = 0

At the point (2, 4),  f 'x(2, 4) = 1 - 2 x 2 = -3

At the point (-2, 4),  f 'x(-2, 4) = 1 - (-2) x (-2) = -3

At the point (3,9),  f 'x(2, 4) = 1 - 3 x 3 = -8

At the point (-3, 9),  f 'x(-2, 4) = 1 - (-3) x (-3) = -8

Something wrong?

f (x, y) = y - x²

First with respect "only" to 'x' 

f 'x(x, y) = y - 2x

This is wrong as 'y' should be treated as a constant (no rate change) with respect to 'x'. so

f 'x(x, y) = 0 - 2x = - 2x

We can differentiate with respect to 'x' as follows:

f 'x(x, y) = d/dx (y- x²) = dy/dx - dx²/dx = dy/dx - 2x

if f (x, y) = y- x² = 0

dy/dx - 2x = 0

dy/dx = 2x

this is correct.


while  with respect "only" to 'y'

f 'y(x, y) = 1 - x²

This is wrong as 'x' should be treated as a constant (no rate change) with respect to 'y'. so

f 'y(x, y) = 1 - 0 = 1


We can differentiate ) with respect to 'x' as follows:

f 'x(x, y) = d/dx (y- x²) = dy/dx - dx²/dx = dy/dx - 2x

if f (x, y) = y- x² = 0

dy/dy - d x²/dy = 0

1 - dx²/dy = 0

 dx²/dy =1

(dx²/dx) (dx/dy) = 1  (Chane rule)

2x (dx/dy) = 1

dx/dy = 1/2x  (please recall dy/dx = 2x)

This is a reciprocal function of  'y = 2x'.

Meanwhile we can proceed as follows:

y =  x²

              __               1/2
x = +/- √ y   =  +/- y

                                 -1/2
x' (f'(x) = +/- (1/2) y 

                         1
             = +/-  ------_
                         2  √ y




Now we will be back to
 

f 'x(x, y) + f 'y(x, y) = -2xi  + 1j = -2xi + j

This is the gradient of f (x, y) = y- x² or this is the gradient f (x, y) = y- x² = 0.  

The slope or tangent is <-2x / +1> or <-2x> and

 the magnitude is
   ______
 √4x² + 1 .

The slope and the magnitude are a function of x.


y - x² = 0

y- x² = z = 0

and take 'z' as the vertical axis to the x-y horizontal plane, 'z' is regarded as height, which means that any place (point) on y= x² is zero (no height, or sticking on the x-y plane). If we take a color (instead of height, the sane scalar value becomes a constant color, say 'red'. So the color of or on y= x² is all 'red'. Color is regarded to represent another dimension, independent but related with y= x². See below:

2-Dimensional Gradient v. 1.2
April 26, 2009 - 15:24 — Charles Belov
2-Dimensional Gradient (2DG) produces a new layer containing a gradient that changes in two dimensions. People using non-English-language GIMP installations are encouraged to upgrade to this version.
9 sample gradients follow (collected into a single image):


We will be back to z (vertical axis) idea.


            z   l         /
                 l       /
                 l     /
                 l   /
                 l /
________ l ___________
               /l                     x
             /  l       
           /    l         
         /      l            
y(+)/        l            


This is the 3D representation.

y- x² = 0 is just in case of z = 0 while z can take any value but a constant (scalar) value.

Let's take some actual values of f (x,y) = y- x² = 0

When x = 0, y = 0

When x = 1, y = 1. When x = -1, y = 1 as well

When x = 2, y = 4. When x = -2, y = 4.

Actually the above values are all on the y = x² on the x-y plane (z = 0) or y- x² = 0

Now we consider z is not 0. Say z = 1. that is y- x² = 1. Please note that this is not y - x² = 1 or y = x² +1 on the x-y plane. 1 is the value of z axis. Then we take the same procedure as above.

y- x² = 1

When x = 0, y = 1

When x = 1, y = 2. When x = -1, y = 2 as well.

When x = 2, y = 5. When x = -2, y = 5.

 When x = 3, y = 10. When x = -3, y = 10.

If we plot these values all the values are on the y = x² + 1. The value 1 is the value of z
(constant height).

Back to simple x-y plane (2D),  y = x² + 1 means the all the y values are shifted to up by 1 in the direction of the y axis. They do not simply go up by value a to z direction.

Let's try some other values. - z direction, for instance.

y- x² = -1

When x = 0, y = -1

When x = 1, y = 0. When x = -1, y = 0 as well.

When x = 2, y = 3. When x = -1, y = 3

 When x = 3, y = 8. When x = -3, y = 8

If we plot these values all the values are on the y = x² - 1. The value -1 is the value of z
(constant height).

Again back to simple x-y plane (2D), the all the y values are shifted by 1 in the minus direction or <-1> of the y axis. They do not simply go down by 1 value a to the z direction.

If we take all the possible values satisfying y- x² = z (z is now any constant value) we can get a parabola like surface going up along z axis. And the level lines (by cutting this parabola like surface horizontally) are all parabola shape satisfying y- x² = z. The value of z is the height as well as the shifting factor in the y-direction as y = x² + z.

Now we consider a tangent line on this parabola like surface. Let's use the level curve at z = 0, that is on the x-y plane. Actually any z value is OK to find the meaning of a tangent line. The tangent line at the point (1, 1) or (1,1,0) on the x-y plane can be show as y = 2x or y - 2x = 0 or can be as (1, 2, 0). The last one (1, 2, 0) shows the direction of  y = x² at the point (1, 1) or (1,1,0): to the x-direction is 1, y-direction 2, z-direction 0. Since this is not a gradient vector, no magnitude.

Tangent line means the slope or rate change of 'y' with respect to 'x' of y = x² . So moving forward or backward from the point P is always with the same slope. For the vertical direction remains z = 0. The biggest difference from the direction of this slope at P is the perpendicular direction to the tangent line and on the parabola like surface, not straight up- or down- word parallel with z axis.

The direction is OK. How bout the rate change?

The partial derivative of the parabola surface f(x,y) = y - x² = z at the point (1,1,0) is (-2, 1, 0) from (-2x, 1) which is a partial differentiation of f (x,y) = y - x² with z = 0 calculated above (shown below again)

f 'x(x, y) + f 'y(x, y) = -2xi  + 1j = -2xi + j  

 So the rate change is -2 of x-direction and 1 of y direction. (the direction is y = -2x).


Ref: http://www.math.oregonstate.edu/home/programs/undergrad/CalculusQuestStudyGuides/vcalc/grad/grad.html

This article is short and well explained.

"

The Gradient and Directional Derivative 

The gradient of a function w = f (x,y,z) is the vector function:



For a function of two variables z = f(x,y), the gradient is the two-dimensional vector. This definition generalizes in a natural way to functions of more than three variables. 

Examples
For the function z =f (x,y )= 4x²+y². The gradient is



For the function w = g (x,y,z) = exp (xyz) + sin (xy), the gradient is



 
Geometric Description of the Gradient Vector
 
There is a nice way to describe the gradient geometrically. Consider z = f (x,y) = 4x²+y². The surface defined by this function is an elliptical paraboloid. This is a bowl-shaped surface. The bottom of the bowl lies at the origin. The figure below shows the level curves, defined by f (x,y) = c, of the surface. The level curves are the ellipses 4x²+y² = c.


The gradient vector <8x,2y> is plotted at the 3 points (sqrt(1.25),0), (1,1), (0,sqrt(5)). As the plot shows, the gradient vector at (x,y) is normal to the level curve through (x,y). As we will see below, the gradient vector points in the direction of greatest rate of increase of f (x,y)
In three dimensions the level curves are level surfaces. Again, the gradient vector at (x,y,z) is normal to level surface through (x,y,z).

Directional Derivatives
 
For a function z = f (x,y), the partial derivative with respect to x gives the rate of change of f in the x direction and the partial derivative with respect to y gives the rate of change of f in the y direction. How do we compute the rate of change of f in an arbitrary direction?
The rate of change of a function of several variables in the direction u is called the directional derivative in the direction u. Here u is assumed to be a unit vector. Assuming w = f (x,y,z) and u =, we have 



Hence, the directional derivative is the dot product of the gradient and the vector u. Note that if u is a unit vector in the x direction, u=<1,0,0>, then the directional derivative is simply the partial derivative with respect to x. For a general direction, the directional derivative is a combination of the all three partial derivatives.

Example
 
What is the directional derivative in the direction <1,2> of the function z = f (x,y) = 4x²+y² at the point x=1 and y=1. The gradient is <8x,2y>, which is <8,2> at the point x=1 and y=1. The direction u is <2,1>. Converting this to a unit vector, we have <2,1>/sqrt(5). Hence,



Directions of Greatest Increase and Decrease
 
The directional derivative can also be written:



where theta is the angle between the gradient vector and u. The directional derivative takes on its greatest positive value if theta=0. Hence, the direction of greatest increase of f is the same direction as the gradient vector. The directional derivative takes on its greatest negative value if theta = pi (or 180 degrees). Hence, the direction of greatest decrease of f is the direction opposite to the gradient vector.


"

Level Curves

Like the above article, most articles on gradient introduce 'level curves' . The level curve shows the same level or value of <scalar value> in 3D like temperature in a room and hill's height. But we must consider well 'temperature' and 'height'.

Level curves of Temperature

Temperature distribution in a room is 3D. So if we check the location of a certain fix temperature and show the measurement result it may become a curved line in 3D or a curved surface of certain thickness in 3D. Then we measure a different fixed temperature and do the same thing. We can paint them with a certain color to visualize them. Then we get another curved line or curved surface. We can paint them with another color to visualize them. But how to calculate the degree of change of temperature spatially. Another way is to use <projection>.  But this is misleading in this case because we cannot show the heights which are supposed to be continually differ.

f (x, y, z) = c (constant)

Level curves of Heights

This is another story. We can use <projection> as the height is the same.

f (x, y), z = c


sptt